- 支持文件格式包含帕纳科(.xrdml)、布鲁克(.rd)、日本理学(.raw)
- 背景函数使用二阶Chebyshev多项式
- 拟合函数使用Split-Pearson VII函数
- 硅基材料数据处理(主要计算半峰宽)暂处于不可用状态
X射线衍射背景资料
X射线的产生与特性
X射线定义为10 pm~10 nm波长的电磁波,在带电粒子速度快速变化的过程中产生;通常所使用的人造X射线有电子激发和同步辐射光两种。
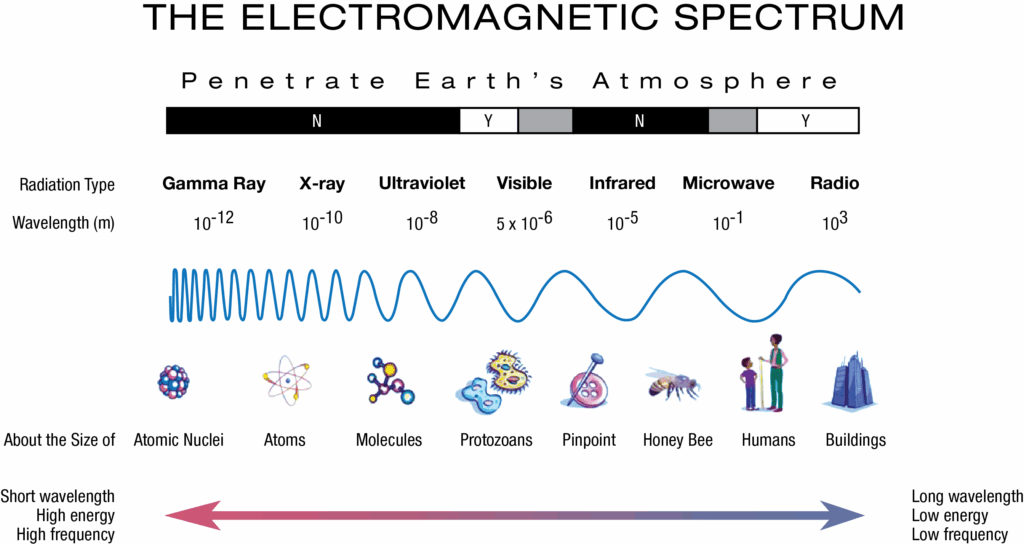
电子激发的X射线使用高能电子轰击靶材;电子在靶材中与靶原子核的库仑场相互作用,经历频繁的加速与减速过程,损失的动能转化为X射线光子,此过程称为韧致辐射,获得的光谱为平滑的连续谱,其短波限由最高电子能量决定,长波部分则与电子的减速过程相关;若电子能量足够高,高能电子将靶原子核内层电子击出,由外层电子跃迁到内层电子位置上,两个能级差产生的能量释放转化为X射线光子,由于同种元素的原子各能级差是一样的,对于同一元素的原子发射出来的X射线波长即时固定的,因此这种形式发生的辐射被称为特征辐射,其发光过程决定了这些谱线不随x射线管的工作条件而变,只取决于阳极靶物质种类,光谱为尖锐的峰。实际物质在电子轰击下发射的X射线光谱为韧致辐射与特征辐射谱线的叠加。
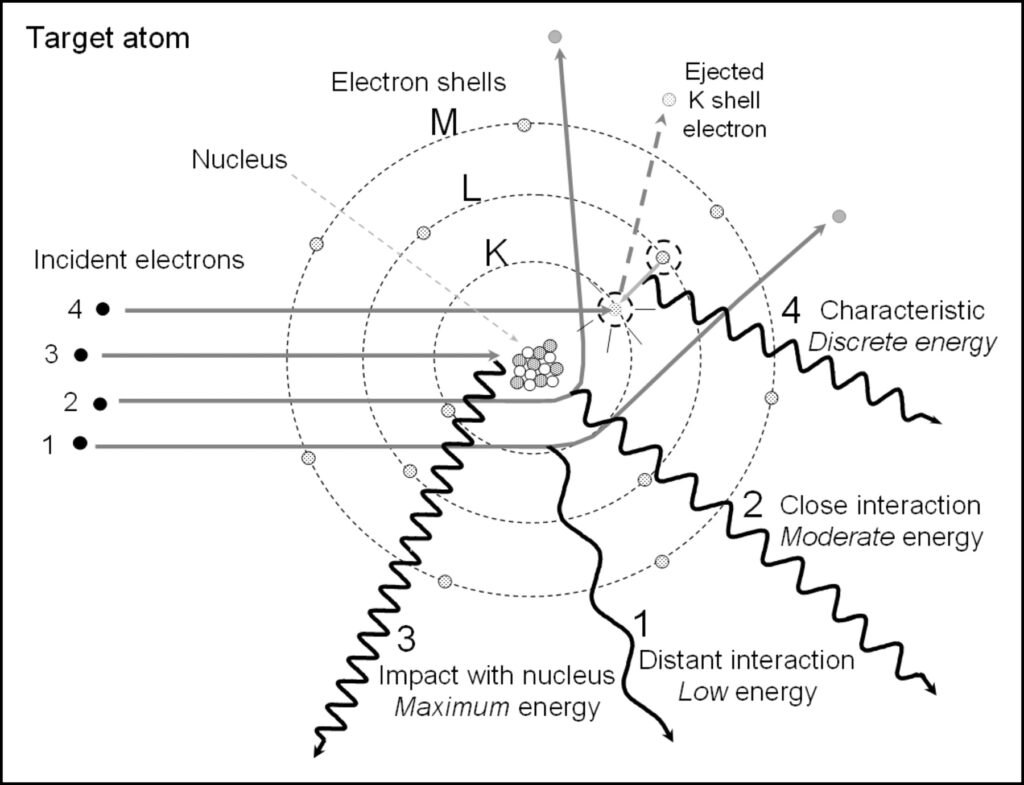
当原子核内K层电子被击出,外层原子跃迁至K层发出的X射线称为K系射线;L层电子被击出,外层原子跃迁至L层发出的X射线称为L系射线;M层电子被击出,外层原子跃迁至M层发出的X射线称为M系射线……
常规XRD衍射仪使用的光源为靶材激发的特征X射线,其各层射线强度比约为K:L:M=100:10:1,且如前述原理可知,K系谱线能量最高,其次为L层……;一般分析所使用的X光源为铜靶、铁靶,其原子序数较低,不足以产生除K系谱线外的特征X射线。
由于外层电子也具有不同的来源,内层电子出现空位时,可能有不同的外层电子来填补,因此K系射线又可进行细分(但是并不是所有外层电子都可以跃迁到内层产生X射线,需要遵守选择定则);Kα射线为电子由L层跃迁到K层产生的射线,M、N层跃迁至K层产生的则称为Kβ;其中Kα又细分为L3跃迁至K层产生的Kα1、L2跃迁至K层产生的Kα2,Kβ细分为M2/M3跃迁至K层产生的Kβ1/Kβ3、N2/N3跃迁至K层产生的Kβ2/Kβ4,各谱线强度比约为Kα1:Kα2:Kβ1/3:Kβ2/4=100:50:15:3;同理,铜靶、铁靶因原子序数较低,仅有Kα1、Kα2、Kβ1/3。
Kβ的存在会导致衍射强度变得混乱,因此需要使用合适的滤光片吸收Kβ,同时保留Kα(使用其他单色器如石墨弯晶单色器等也可达到相同甚至更好效果但成本较高,一般在单晶衍射等精密测试中使用);滤波片材料的原子序数需比靶材的原子序数小1或2(Z<40时取1,Z≥40时取2,如铜靶一般使用镍片滤光),使得其吸收限处于Kα与Kβ之间;通过合理选择滤光片材料种类及厚度,可获得Kα:Kβ>500的光线,即可不考虑Kβ对衍射结果的影响(部分现代衍射仪使用具有能量分辨能力的探测器,可以直接在后端消除Kβ的影响而不需要使用滤光片);同时可以吸收掉大部分的韧致辐射X射线,因此也可以不用考虑连续谱X射线的影响(虽然在实际操作中也可很容易地将其扣除)。
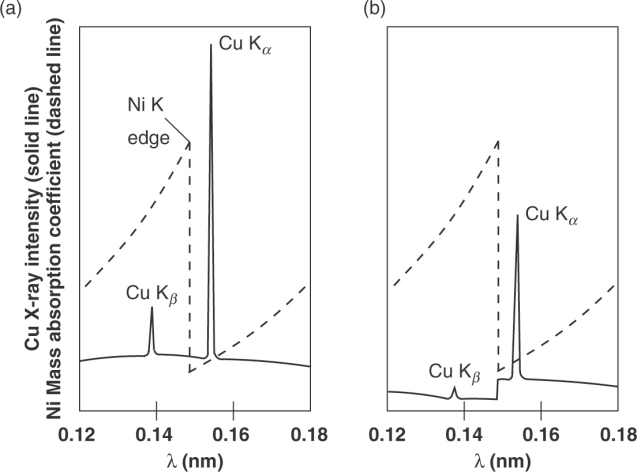
由于Kα谱线的两个精细谱线能量极为接近,使用额外方法在光路中去除其中一个谱线既不经济难度也较大,因此一般选择获得Kα的混合光谱衍射结果,在后端数据处理中对其进行考虑。
衍射及其特性
粉末XRD衍射几何
Bragg-Brentano几何
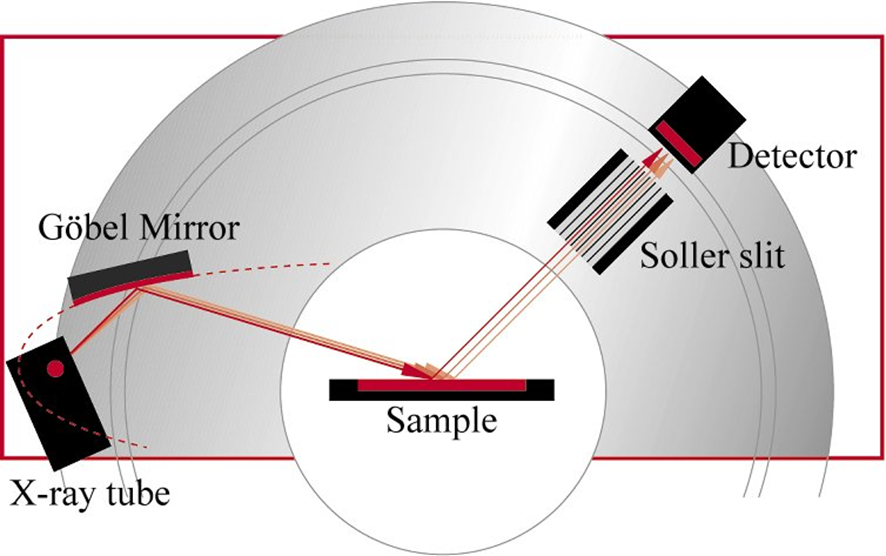
常见的XRD光路是适用于粉末样品的Bragg-Brentano几何(BB几何),其特征为光源与探测器部署于以样品表面中心为圆心的同一半径圆弧上;属平板反射、光路简单、强度高,适合进行高效的定性定量分析。

平行束几何
使用一些特殊形状的反光镜可以将X射线转换为平行光,例如将X射线管阳极置于抛物面镜的焦点上;平行光束能大幅度提高衍射强度,还可以降低衍射峰的仪器本征宽度和峰型不对称因素,因而显著提高衍射峰分辨率和峰形对称性,也有利于织构分析和应力分析。在进行高低温和化学反应研究时,能够消除由于温度变化或化学反应引起的样品面的高度偏移带来的衍射峰位的漂移问题。
粉末XRD衍射谱线的峰型
总体峰型的组成
X射线自身的展宽
理想情况下,特征X射线的光谱应为单一值,但实际情况受到多重因素影响,其光谱呈现出不同程度的展宽;
自然展宽
由于特征辐射为原子内电子从高能级跃迁到低能级的自发辐射,因能量-时间不确定关系,原子在两个能级间跃迁时还会有一定概率吸收和发射具有失谐的光子,这导致了光谱有一定的宽度,称为自然展宽,其线型为洛伦兹函数。
碰撞展宽
原子间碰撞缩短激发态寿命,等效于自然展宽,其线型为洛伦兹函数。
多普勒展宽
也称为热展宽,原子热运动导致发射源与探测器相对速度分布,引起多普勒频移,服从麦克斯韦-玻尔兹曼速率分布,其线型为高斯函数。
固态晶格效应展宽
分为声子展宽(晶格原子热振动导致发射能级微扰,能级位置随时间涨落)与缺陷/应力展宽(晶格缺陷、位错或内应力引起能级分布展宽),其线型为高斯函数。
衍射仪引入的展宽
衍射仪自身引入的展宽包括垂直(于测角仪轴向)发散导致的展宽、光路对准误差导致的展宽等。垂直发散展宽可以使用Sollar狭缝进行限制,而光路对准误差则根据设备几何条件及对光状态不同而产生差异。
粉末样品平板表面导致的展宽
根据欧几里得几何:“同一圆弧上的角是彼此相等的”和“圆心角是同一基底上的圆周角的两倍——即在同一弧上的角相等”。 因此对于圆周上任意两个点S和D,与O点构成的角度角度是常数,无论点O的位置如何。
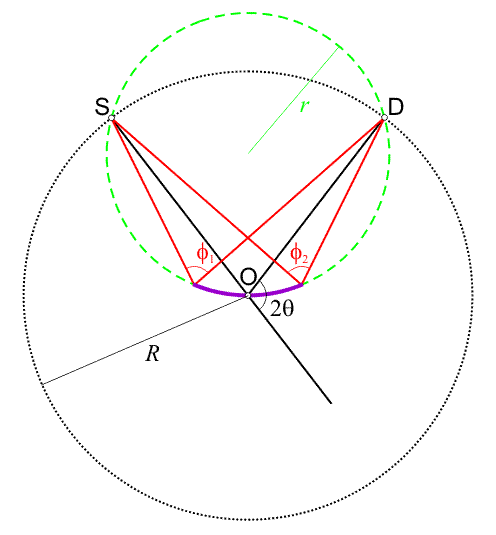
依照欧几里得聚焦几何,样品表面应为一与射线源、探测器、测角仪中心三点相接的内接圆;例如在上图中,中心样品呈弯曲状,且为了实现完美聚焦,曲率必须根据散射角2θ 变化,而这对于平板支架中的粉末样品来说是不可能的。实际应用中,样品表面是完全平坦的,因此衍射光束的聚焦效果并不是理想的,这会对衍射图谱中峰的宽度产生一定的影响。
但是上图是被高度夸大的,因为入射光束在样品上的覆盖范围过大,一般粉末衍射测试时会使用非常小的发散狭缝及接收狭缝。此外,随着样品角 θ 的增加,光斑覆盖范围会显著减小。因此,这种展宽的影响并没有那么显著。
粉末样品对光线吸收导致的展宽
粉末样品本身性质导致的展宽
粉末样品本身的性质也会造成衍射线型的展宽,主要的影响因素有不完美晶格导致的展宽、晶粒尺寸导致的展宽、应力作用导致的展宽。
使用到的数学工具
卷积(Convolution)
反卷积(Deconvolution)
拟合(Fitting)
文件读取部分
不同衍射仪厂家的衍射数据有着不同的格式,对数据的读取、转换是数据处理的第一步。
.xrdml文件为帕纳科公司XRD设备产生的数据文件,其使用xml语言格式,可读性较强,可以较为简单地进行读取。需要注意的是,各衍射数据角度需通过文件内记录的起始位置、终止位置及步长进行计算,不同软件(MDI Jade、X'Pert HighScore)的读取结果可能存在差异,通过与原厂软件(X'Pert HighScore)比对,确认角度应使用以下代码中的转换逻辑。
# .xrdml 读取模块
# .xrdml 读取模块
class XRDMLReader(BaseReader):
@staticmethod
def read_data(file_path):
try:
"""读取.xrdml文件并返回处理后的数据"""
DOMTree = xml.dom.minidom.parse(file_path)
collection = DOMTree.documentElement
scan_start = float(collection.getElementsByTagName('startPosition')[0].childNodes[0].data)
scan_end = float(collection.getElementsByTagName('endPosition')[0].childNodes[0].data)
if collection.getElementsByTagName('counts') != []:
data_point = collection.getElementsByTagName('counts')[0].childNodes[0].data.split(" ")
else:
data_point = collection.getElementsByTagName('intensities')[0].childNodes[0].data.split(" ")
scan_number = len(data_point)
scan_step = (scan_end - scan_start) / (scan_number - 1)
scan_x = np.array([scan_start + i * scan_step for i in range(scan_number)])
scan_y = np.array([float(pt) for pt in data_point])
return scan_x, scan_y
except RuntimeError as e:
print(f"读取失败: {e}")
return None, None
except xml.parsers.expat.ExpatError as e:
return None, None.rd文件为飞利浦公司XRD设备产生的数据文件,帕纳科公司是思百吉集团旗下的分析仪器公司,前身为飞利浦公司分析仪器部,因此帕纳科XRD设备沿用其文件格式,导出数据时也可以导出.rd文件。文件为二进制文件,读取逻辑如下。
# .rd 读取模块
# .rd 读取模块
class PhilipsRDReader(BaseReader):
@staticmethod
def read_data(file_path):
"""读取.rd文件并返回处理后的数据"""
with open(file_path, 'rb') as f:
head = f.read(4)
if head not in [b"V3RD", b"V5RD"]:
raise ValueError("无效的RD文件")
f.seek(214)
x_step = np.frombuffer(f.read(8), dtype=np.float64)[0]
x_start = np.frombuffer(f.read(8), dtype=np.float64)[0]
x_end = np.frombuffer(f.read(8), dtype=np.float64)[0]
pt_cnt = int((x_end - x_start) / x_step)
f.seek(810 if head == b"V5RD" else 250)
ycol = np.frombuffer(f.read(pt_cnt * 2), dtype=np.uint16)
ycol = 0.01 * ycol * ycol
xcol = np.linspace(x_start + x_step / 2, x_end - x_step / 2, pt_cnt)
return xcol, ycol.raw文件在本文中特指日本理学XRD设备产生的数据文件(该扩展名应用较多,其他设备也可能导出.raw后缀的二进制文件,不确定转换逻辑是否相同),读取逻辑如下。
# 理学 .raw 读取模块
# 理学 .raw 读取模块
class RigakuRawReader(BaseReader):
@staticmethod
def read_data(file_path):
try:
with open(file_path, 'rb') as f:
header = f.read(3158)
f.seek(0x0B92)
start_angle = struct.unpack('<f', f.read(4))[0]
f.seek(0x0B96)
end_angle = struct.unpack('<f', f.read(4))[0]
f.seek(0x0B9A)
step = struct.unpack('<f', f.read(4))[0]
num_points = int(round((end_angle - start_angle) / step)) + 1
scan_x = np.arange(start_angle, end_angle + step/2, step)
f.seek(0x0C56)
scan_y = []
for _ in range(num_points):
value = struct.unpack('<f', f.read(4))[0]
scan_y.append(value)
scan_y = np.array(scan_y)
return scan_x, scan_y
except RuntimeError as e:
print(f"读取失败: {e}")
return None, NoneKα2校正
Kα2的去除使用迭代法;
迭代开始前:
- 计算每个点位对应Kα1和Kα2的角度
- 如果函数有传入初始值,使用传入量,否则将原始曲线作为Kα1曲线迭代初始值
迭代过程:
- 计算背景值(使用前30个数据点的平均值)
- 创建Kα1强度的插值函数
- 估计Kα2强度(假设Kα2强度是Kα1强度的一半)
- 只保留有效数据点的Kα2强度
- 从原始强度中减去Kα2强度得到校正后的强度
- 确保校正后的强度非负
- 重复上述过程指定次数(默认8次)
# 迭代法Kα2校正
def correct_ka2(two_theta, intensity, intensity_0=None, lambda_ka1=1.54056, lambda_ka2=1.54439, iterations=8):
theta_rad = np.radians(two_theta / 2)
sin_theta_ka1 = np.sin(theta_rad)
sin_theta_ka2 = sin_theta_ka1 * (lambda_ka1 / lambda_ka2)
valid = sin_theta_ka2 <= 1.0
theta_ka2_rad = np.arcsin(sin_theta_ka2, where=valid, out=np.zeros_like(sin_theta_ka2))
two_theta_ka2 = np.degrees(theta_ka2_rad) * 2
if intensity_0 == None:
corrected_intensity = intensity.copy()
else:
corrected_intensity = intensity_0
for _ in range(iterations):
bg_fill = np.mean(corrected_intensity[:30])
ka1_interp = interp1d(two_theta, corrected_intensity, kind='linear', bounds_error=False, fill_value=bg_fill)
ka2_intensity = ka1_interp(two_theta_ka2) * 0.5
ka2_intensity *= valid
corrected_intensity = np.clip(intensity - ka2_intensity, 0, None)
return two_theta, corrected_intensity为了后续需求,增加了一个在已有数据中回添Kα2强度的函数,与上述过程相反,且不需要迭代过程。
# 回添Kα2强度
def decorrect_ka2(two_theta, intensity, lambda_ka1=1.54056, lambda_ka2=1.54439):
theta_rad = np.radians(two_theta / 2)
sin_theta_ka1 = np.sin(theta_rad)
sin_theta_ka2 = sin_theta_ka1 * (lambda_ka1 / lambda_ka2)
theta_ka2_rad = np.arcsin(sin_theta_ka2)
two_theta_ka2 = np.degrees(theta_ka2_rad) * 2
ka2_intensity = np.interp(two_theta_ka2, two_theta, intensity) * 0.5
decorrected_intensity = intensity + ka2_intensity
return decorrected_intensity基础函数定义
Lorentzian 函数
作为概率分布,通常叫作柯西分布,物理学家也将之称为洛伦兹分布或者Breit-Wigner分布。在物理学中的重要性很大一部分归因于它是描述受迫共振的微分方程的解。在光谱学中,它描述了被共振或者其它机制加宽的谱线形状。1
其概率密度函数如下:
简化峰型函数为:$$f_{\text{Lorentz}}(x; a, x_0, w) = \frac{a}{1 + (\frac{x - x_0}{w})^2}$$
# Lorentzian 函数
def lorentzian(x: np.ndarray, amplitude: float, center: float, sigma: float) -> np.ndarray:
return amplitude / (1 + ((x - center) / sigma)**2)Gaussian 函数
正态分布,物理学中通称高斯分布,是一个非常常见的连续概率分布。正态分布在统计学上十分重要,经常用在自然和社会科学来代表一个不明的随机变量。中心极限定理指出,在特定条件下,一个具有有限均值和方差的随机变量的多个样本(观察值)的平均值本身就是一个随机变量,其分布随着样本数量的增加而收敛于正态分布。因此,许多与独立过程总和有关的物理量,例如测量误差,通常可被近似为正态分布。2
其概率密度函数如下:
简化峰型函数为:$$f_{\text{Gaussian}}(x; a, x_0, w) = a * e^{-(\frac{x - x_0}{w})^2}$$
# Gaussian 函数
def gaussian(x: np.ndarray, amplitude: float, center: float, sigma: float) -> np.ndarray:
return amplitude * np.exp(-((x - center) / sigma)**2)Pseudo-Voigt 函数
通常情况下,当同时存在高斯展宽及洛伦兹展宽的时候,其最终结果为多重展宽的卷积,即Voigt函数;
其概率密度函数如下:
由于早期计算机技术限制,卷积函数计算困难,通常使用算法上更容易实现的pseudo-Voigt 函数进行近似,pV函数是高斯函数和洛伦兹函数的线性组合;
其概率密度函数如下:
# Pseudo-Voigt 函数
def pseudo_voigt(x: np.ndarray, amplitude: float, center: float, sigma: float, eta: float) -> np.ndarray:
return eta * lorentzian(x, amplitude, center, sigma) + (1 - eta) * gaussian(x, amplitude, center, sigma)Split-Pearson VII 函数
Pearson VII函数
其概率密度函数如下:
Split-Pearson VII 函数则为两侧具有不同形状参数的 Pearson VII 函数,用于对偏态分布进行更好的拟合。
# Split-Pearson VII 函数
def split_pearson_vii(x: np.ndarray, a: float, x0: float, w_L: float, w_R: float, m: float) -> np.ndarray:
return np.where(
x <= x0,
a / (1 + (4 * (x - x0)**2 / w_L**2) * (2**(1/m) - 1))**m,
a / (1 + (4 * (x - x0)**2 / w_R**2) * (2**(1/m) - 1))**m
)Chebyshev 多项式
# 二阶Chebyshev 多项式
def chebyshev(x: np.ndarray, c0, c1, c2):
return Chebyshev([c0, c1, c2])(x)数据拟合
细究衍射峰型的具体数学表示费时费力且收益不大,对于工程应用,了解原理后使用合适的函数对衍射数据进行拟合且获得残差较小的结果是足够的。
拟合路径设计
如果所获得的衍射数据是纯粹的,那拟合路径有且只有一条,但因为往往获得的数据是混合了Kα2的成分,因此拟合路径分野成以下两种:
先进行Kα2分离,使用分离后的“纯净”衍射数据拟合
graph LR
A[数据读取] --> B[Kα2分离]
B --> C[使用纯净衍射数据拟合]
C --> D[处理拟合结果]先假定峰参数,将假定的参数计算为拟合曲线后,将Kα2强度加回,使用新的混合函数对原始衍射数据进行拟合
graph LR
A[数据读取] --> B[构建拟合函数]
B --> C[将拟合函数改为含有Kα2的新函数]
C --> D[使用原始衍射数据拟合]
D --> E[处理拟合结果]拟合模型设计
经过实际数据的验证,拟合模型使用二阶切比雪夫多项式作为背景,在低角度下使用Split-Pearson VII 函数作为峰函数是合适的;那么对于有硅内标的D002衍射数据,其拟合模型可构建为:
# 定义双峰拟合函数(Split-Pearson VII 峰 + 二阶切比雪夫背景)
def double_peak(x, a1, x01, w_L1, w_R1, m1, a2, x02, w_L2, w_R2, m2, c0, c1, c2):
# 两个 Split-Pearson VII 峰 + 二阶切比雪夫背景
return (split_pearson_vii(x, a1, x01, w_L1, w_R1, m1) + split_pearson_vii(x, a2, x02, w_L2, w_R2, m2) + chebyshev(x, c0, c1, c2))那么,对应的使用原始衍射数据进行拟合的函数可构建为:
# 定义双峰拟合函数(Split-Pearson VII 峰 + 二阶切比雪夫背景 + Kaplha2)
def double_peak_raw(x, a1, x01, w_L1, w_R1, m1, a2, x02, w_L2, w_R2, m2, c0, c1, c2):
# 回添Kα2强度
def decorrect_ka2(two_theta, intensity, lambda_ka1=1.54056, lambda_ka2=1.54439):
theta_rad = np.radians(two_theta / 2)
sin_theta_ka1 = np.sin(theta_rad)
sin_theta_ka2 = sin_theta_ka1 * (lambda_ka1 / lambda_ka2)
theta_ka2_rad = np.arcsin(sin_theta_ka2)
two_theta_ka2 = np.degrees(theta_ka2_rad) * 2
ka2_intensity = np.interp(two_theta_ka2, two_theta, intensity) * 0.5
decorrected_intensity = intensity + ka2_intensity
return decorrected_intensity
# 两个 Split-Pearson VII 峰 + 二阶切比雪夫背景
return decorrect_ka2(x,(split_pearson_vii(x, a1, x01, w_L1, w_R1, m1) + split_pearson_vii(x, a2, x02, w_L2, w_R2, m2) + chebyshev(x, c0, c1, c2)))关于机器宽化的分离
实际获得的衍射峰型是样品本身展宽(晶粒尺寸&应力展宽)与机器展宽的叠加,想要单独获得样品本身峰宽,通过实测衍射峰与机器展宽函数进行反卷积即可;精确地机器展宽需要通过一系列标定获得,过程复杂且所用标样有很高的成本;但是对于前述带内标的负极材料来说,机器展宽可以通过配置的硅内标本身近似获得。

Comments NOTHING